以前「ベルヌーイ分布と二項分布」という記事を書きましたが、ポアソン分布はこの二項分布と大きな関係があります。ポアソン分布は二項分布をある特殊な条件化で考えた時の分布なのです。それでは1つずつ確認していきましょう。
ポアソン分布の概要
二項分布における\(n\)が十分に大きく、確率\(p\)が十分に小さいときに、平均\(np=\lambda\)のポアソン分布に近似できます。言い換えると、「稀に起こる事象が一定時間あたりに起こる回数」が従う分布です。例えば、「1日あたりの交通事故死亡者数」がポアソン分布に従うことが知られています。
ポアソン分布の定義
ポアソン分布の定義は次の通りです。
非負整数値をとる確率変数\(X\)が、パラメータ\(\lambda>0\)に対して
P(X=k) = \frac{\lambda^{k}e^{-\lambda}}{k!},\quad k=0,1,2\cdots
$$
を確率関数として持つとき、\(X\)の分布をポアソン分布(Poisson distribution)といいます。また、\(Po(\lambda)\)と表記します。
期待値と分散
ポアソン分布の期待値と分散は次の通りです。
\(X\)はパラメータ\(\lambda\)のポアソン分布\(Po(\lambda)\)に従うとする。
\begin{align}
E[X] &= \lambda\\
V[X] &= \lambda
\end{align}
$$
ポアソン分布の期待値と分散はどちらも\(\lambda\)なのです。覚えやすいですね。
証明)
\begin{align}
E[X] &= \sum^{\infty}_{k=0}k\frac{\lambda^k e^{-\lambda}}{k!}\\
&= \sum^{\infty}_{k=1}\frac{\lambda\cdot\lambda^{k-1} e^{-\lambda}}{(k-1)!}\\
&= \lambda\sum^{\infty}_{k=1}\frac{\lambda^{k-1} e^{-\lambda}}{(k-1)!}\\
&= \lambda
\end{align}
$$
\begin{align}
E[X^2] &= \sum^{\infty}_{k=0}k^2\frac{\lambda^k e^{-\lambda}}{k!}\\
&= \sum^{\infty}_{k=0}k\frac{\lambda\cdot\lambda^{k-1} e^{-\lambda}}{(k-1)!}\\
&= \sum^{\infty}_{k=0}\{(k-1)+1\}\frac{\lambda\cdot\lambda^{k-1} e^{-\lambda}}{(k-1)!}\\
&= \sum^{\infty}_{k=0}(k-1)\frac{\lambda\cdot\lambda^{k-1} e^{-\lambda}}{(k-1)!} + \frac{\lambda\cdot\lambda^{k-1} e^{-\lambda}}{(k-1)!}\\
&= \lambda^2\sum^{\infty}_{k=2}\frac{\lambda^{k-2} e^{-\lambda}}{(k-2)!} + \lambda\sum^{\infty}_{k=1}\frac{\lambda^{k-1} e^{-\lambda}}{(k-1)!}\\
&=\lambda^2 + \lambda
\end{align}
$$
\begin{align}
V[X] &= E[X^2] – (E[X])^2\\
&= (\lambda^2 + \lambda) – \lambda^2\\
&= \lambda
\end{align}
$$
二項分布からポアソン分布の導出
冒頭で述べたようにポアソン分布は二項分布をある条件下で考えたときの極限として得られます。
二項分布\(Bin(n,p)\)の期待値は\(E[X]=np\)でしたね。そこで次のような条件を考えます。
- \(np \rightarrow \lambda (一定 > 0)\)
- \(n\rightarrow\infty\Leftrightarrow p\rightarrow0\)
この条件のもとで二項分布の極限はポアソン分布となります。また、この法則をポアソンの少数の法則といいます。
証明)
\begin{align}
\lim_{n\rightarrow\infty}{_nC_k}p^{k}(1-p)^{n-k}
&=\lim_{n\rightarrow\infty}\frac{n!}{k!(n-k)!}\left(\frac{\lambda}{n}\right)^k\left(1-\frac{\lambda}{n}\right)^{n-k}\\
&=\lim_{n\rightarrow\infty}\frac{1}{k!}\cdot\frac{n!}{(n-k)!}\cdot\frac{\lambda^k}{n^k}\cdot\left(1-\frac{\lambda}{n}\right)^n\left(1-\frac{\lambda}{n}\right)^{-k}\\
&=\lim_{n\rightarrow\infty}
\frac{\lambda^k}{k!}\left(1-\frac{\lambda}{n}\right)^n
\frac{n!}{(n-k)!}\cdot\frac{1}{n^k}\left(1-\frac{\lambda}{n}\right)^{-k}\\
&=\lim_{n\rightarrow\infty}
\frac{\lambda^k}{k!}\left(1-\frac{\lambda}{n}\right)^n
\underbrace{\frac{n}{n}\cdot\frac{n-1}{n}\cdots\frac{n-k+1}{n}}_{k個}\left(1-\frac{\lambda}{n}\right)^{-k}\\
&=\frac{\lambda^{k}e^{-\lambda}}{k!}
\end{align}
$$
\begin{align}
\lim_{n\rightarrow\infty}\left(1-\frac{\lambda}{n}\right)^n
&= \lim_{n\rightarrow\infty}\left\{1-\left(\frac{1}{n/\lambda}\right)\right\}^n\\
&= \lim_{n\rightarrow\infty}\left[\left\{1-\left(\frac{1}{n/\lambda}\right)\right\}^{\frac{n}{\lambda}}\right]^\lambda\\
&= \lim_{n\rightarrow\infty}\left[\left\{1-\left(\frac{1}{n/\lambda}\right)\right\}^{\frac{n}{\lambda}}\right]^\lambda\\
&=e^{-\lambda}
\end{align}
$$
ポアソン分布の正規近似
ポアソン分布はパラメータ\(\lambda\)が大きくなるにつれて正規分布に近づくという性質があります。その動きを可視化してみました。左がポアソン分布であり、右が正規分布です。これを見ると\(\lambda\) が大きくなるにつれて正規分布に近づいていく様子がよくわかると思います。
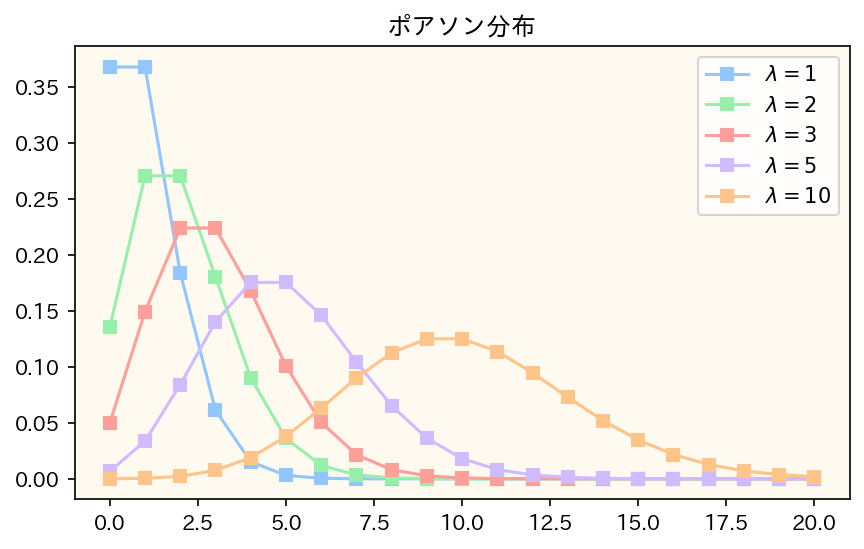
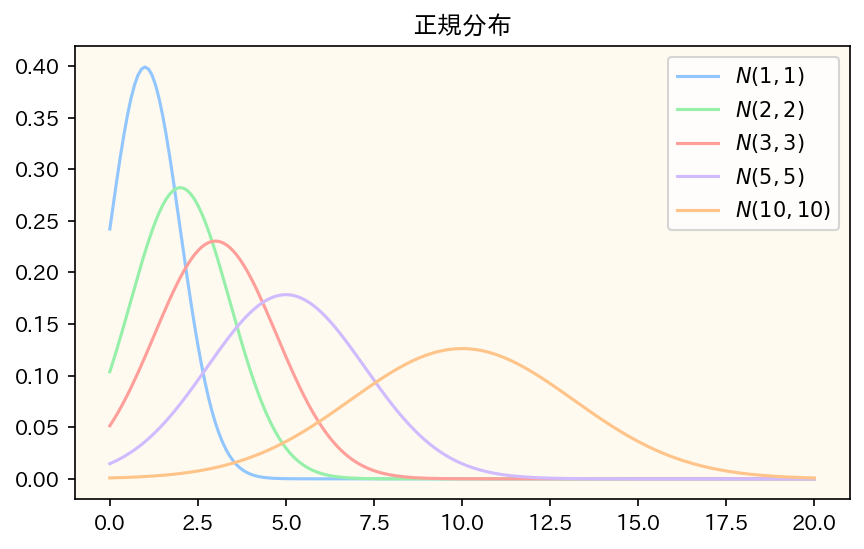
- ポアソン分布は「\(np = \lambda, n\rightarrow\infty\)」という条件のもと二項分布の極限から得られる分布
- 期待値と分散はどちらも\(\lambda\)
- \(\lambda\)が大きくなるにつれて正規分布に近づく
今回は以上です。ポアソン分布の期待値や分散の導出の仕方は他にもあるのでぜひもう一つの方法でも証明をしてさらに理解を深めてみてください!


コメント