今回は求根アルゴリズムの一つであるニュートン・ラフソン法をPythonを用いた実装で理解していこうと思います。
ニュートン・ラフソン法とは?
ニュートン・ラフソン法(Newton-Raphson Method)とは、関数\(f(x)\)が\(0\)となる根\(x_{root}\)の近似根を反復計算により得る方法です。具体的には次のような更新式を用いて反復計算を行います。
関数\(f(x)\)が定義域(探索区域)で微分可能なとき、更新点を\(x_{n+1}\)とすれば、ニュートン・ラフソン法の更新式は次のように表されます。
x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}
$$
更新式の導出
ニュートン・ラフソン法では関数\(f(x)\)の1次近似を用いて更新していきます。ですので、更新式の導出にあたり、まずは\(f(x)\)の\(a\)点周りのテイラー展開を1次の項まで行います。
f(x) = f(a) + f'(a)(x-a)+o((x-a))\approx f(a) + f'(a)(x-a)
$$
これが\(a\)点周りの関数\(f(x)\)の1次近似です。つまり、更新点はこの近似式が\(0\)となる点ですので、更新点を\(x_{n+1}\)、現在点を\(x_n\)とすると
\begin{align}
f(x_n) + f'(x_n)(x_{n+1}-x_n) &= 0\\
f(x_n) + f'(x_n)x_{n+1} – f'(x_n)x_n&= 0\\
f'(x_n)x_{n+1} &= f'(x_n)x_n -f(x_n)\\
x_{n+1} &= x_n -\frac{f(x_n)}{f'(x_n)}\\
\end{align}
$$
となり、先ほどの更新式が導出できました。
更新はいつまでするの?
更新式がわかったけど、それをいつまで行うのかという話ですよね。終了条件は、「更新点を関数\(f(x)\)に代入したときの値がある一定の値より小さくなったら」です。ある一定の値は計算機などによって自然に定まる丸め誤差限界の場合や自分で設定するなどの場合があります。
ニュートン・ラフソン法の可視化
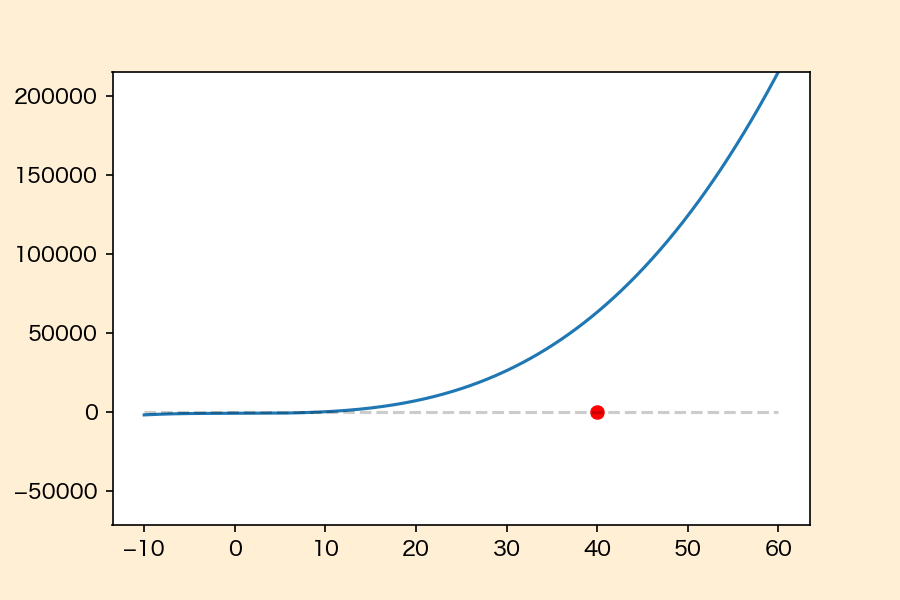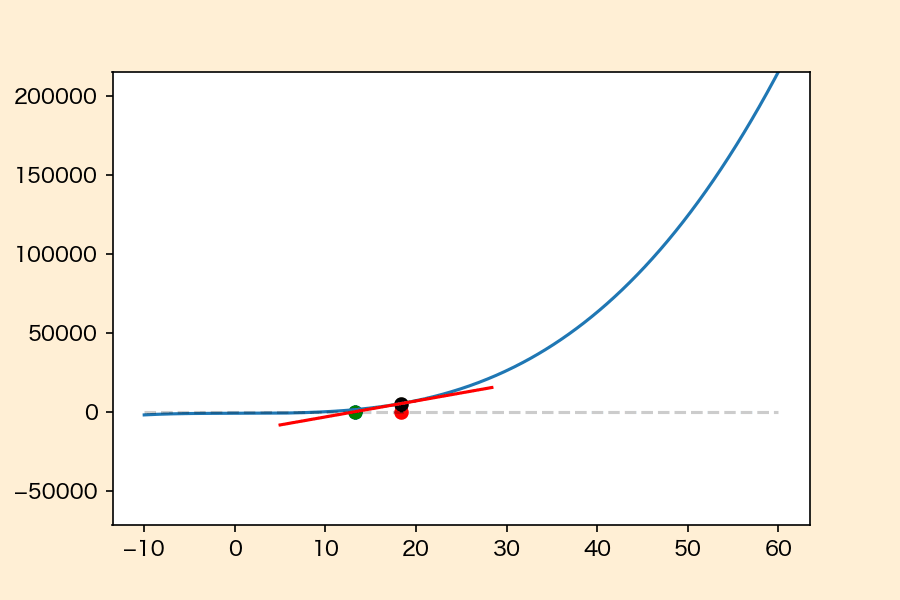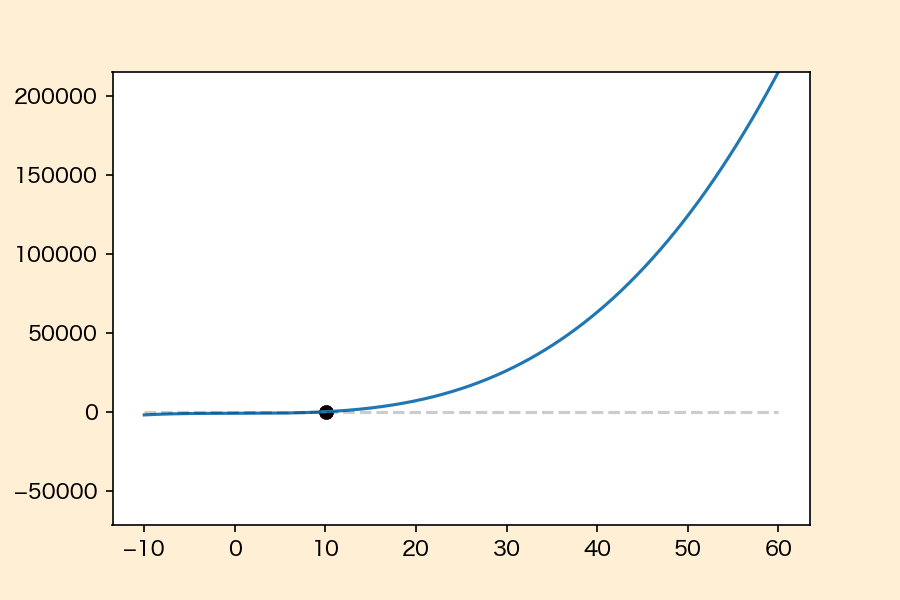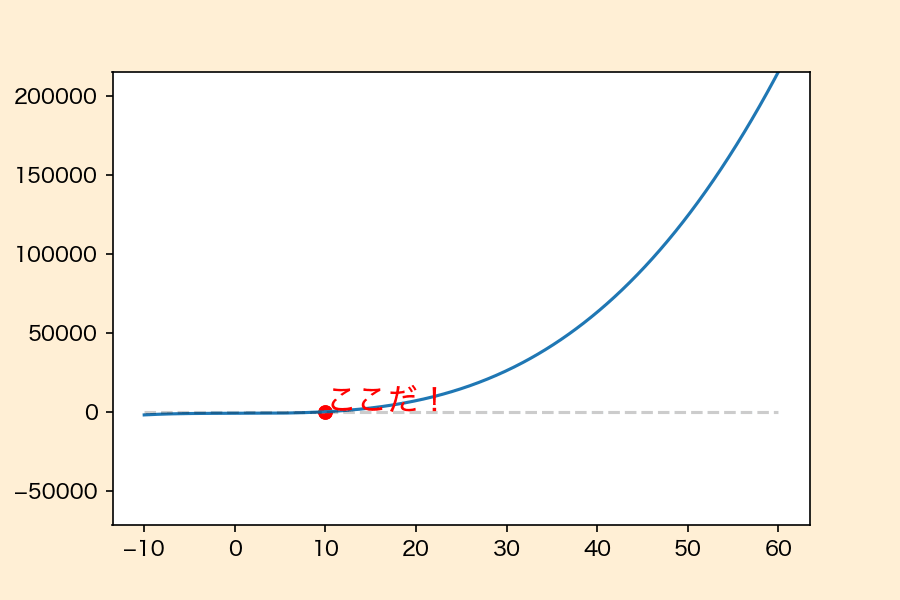
ニュートン・ラフソン法がどのような動きなのかを\(f(x) = x^3 – 1000\)という関数の根を求めるときを例に可視化すると下のようになります。
●:現在点 ●:更新点
Pythonによる実装
ニュートン・ラフソン法では微分を使うので、まずは微分の定義をします。
def differential_calculus(func, x, dx=1e-6):
'''
func : 関数
x : x座標
dx : 無限小
-----------
return : 点xにおける微分係数
'''
f_prime = (func(x + dx) - func(x - dx)) / (2 * dx)
return f_primeここで、定義した微分を用いてニュートン・ラフソン法を定義する。
def newton_raphson_method(func, x, epsilon=1e-6):
'''
func : 関数
x : 初期値
epsilon : 要求精度
'''
while abs(func(x)) > epsilon:
f_prime = differential_calculus(func, x)
x = x - func(x) / f_prime
return xすると、先ほど可視化した関数\(f(x) = x^3 – 1000\)の根は
func = lambda x: x**3 - 1000
x_root = minimize.newton_raphson_method(func, 15)
print(f'根は {x_root} です')
print(f'実際に関数に代入すると {func(x_root)}' です)【出力結果】
根は 10.000000000000114 です
実際に関数に代入すると 3.410605131648481e-11 ですこのようにして、ニュートン・ラフソン法を用いて関数の根を求めることができました。


コメント