今回は尤度を可視化することでさらに理解を深めようと思います。
尤度とは
尤度(likelihood)とは、ある観測値が得られたときに、その観測値が従うとされる確率密度関数または確率質量関数から得られる観測値としてどのくらい尤もらしいかを表します。また、確率密度関数または確率質量関数のパラメータが未知であるとき、そのパラメータを変数として表現した尤度を尤度関数(likelihood function)と言います。
確率変数列 \({X} = (X_1,X_2,\cdots,X_n)\) は独立同一にパラメータ\(\theta\)の分布に従うとします。この確率変数の観測値として \({x} = (x_1,x_2,\cdots,x_n)\) が得られたとき、確率密度関数(確率質量関数)を\(f(x;\theta)\)とすると尤度関数は次のようになります。
L(\theta\:; x) = \prod_{x} f(x_i;\theta)
$$
ここで、確率密度関数\(f(x_i;\theta)\)は観測値\(x_i\)の関数であり、尤度関数\(L(\theta\:;x)\)はパラメータ\(\theta\)の関数であるということに注意してください。
尤度関数の可視化
それでは、尤度関数を可視化していきます。それに伴い、次のような状況を考えます。
二項分布\(Bin(20, p)\)に従うと知られている事象から次のような観測値がえられました。
x = (1, 2, 3, 4, 4, 5, 5, 6, 7, 4, 3)
$$
このとき、得られた観測値のヒストグラムは次のようになります。(解説をしやすくするために都合がいい観測値を考えました)
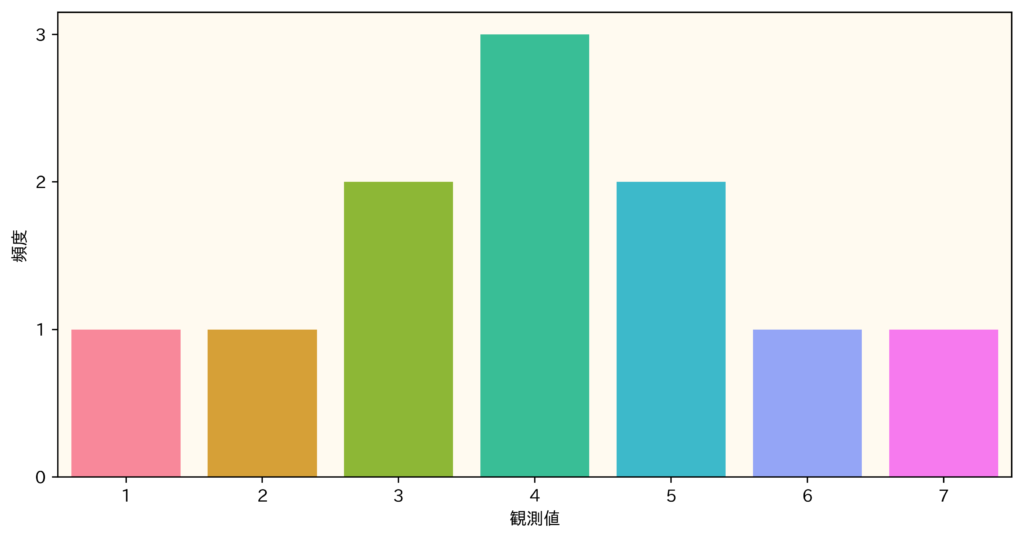
この観測値を得たときの尤度関数のグラフを見てみましょう。尤度関数はパラメータ\(\theta\)の関数でした。二項分布のパラメータは試行回数\(n\)と成功確率\(p\)でした。今回は\(n=20\)という状況から得られた観測値ですので、尤度関数は次のようになると考えられます。
\begin{align}
L(p\:; x) &= \prod_{x} P(x_i;p)\\
&= \prod_{x} {_{20}C_{x_i}}p^{x_i}(1-p)^{20-x_i}\quad(0\le p \le1)
\end{align}
$$
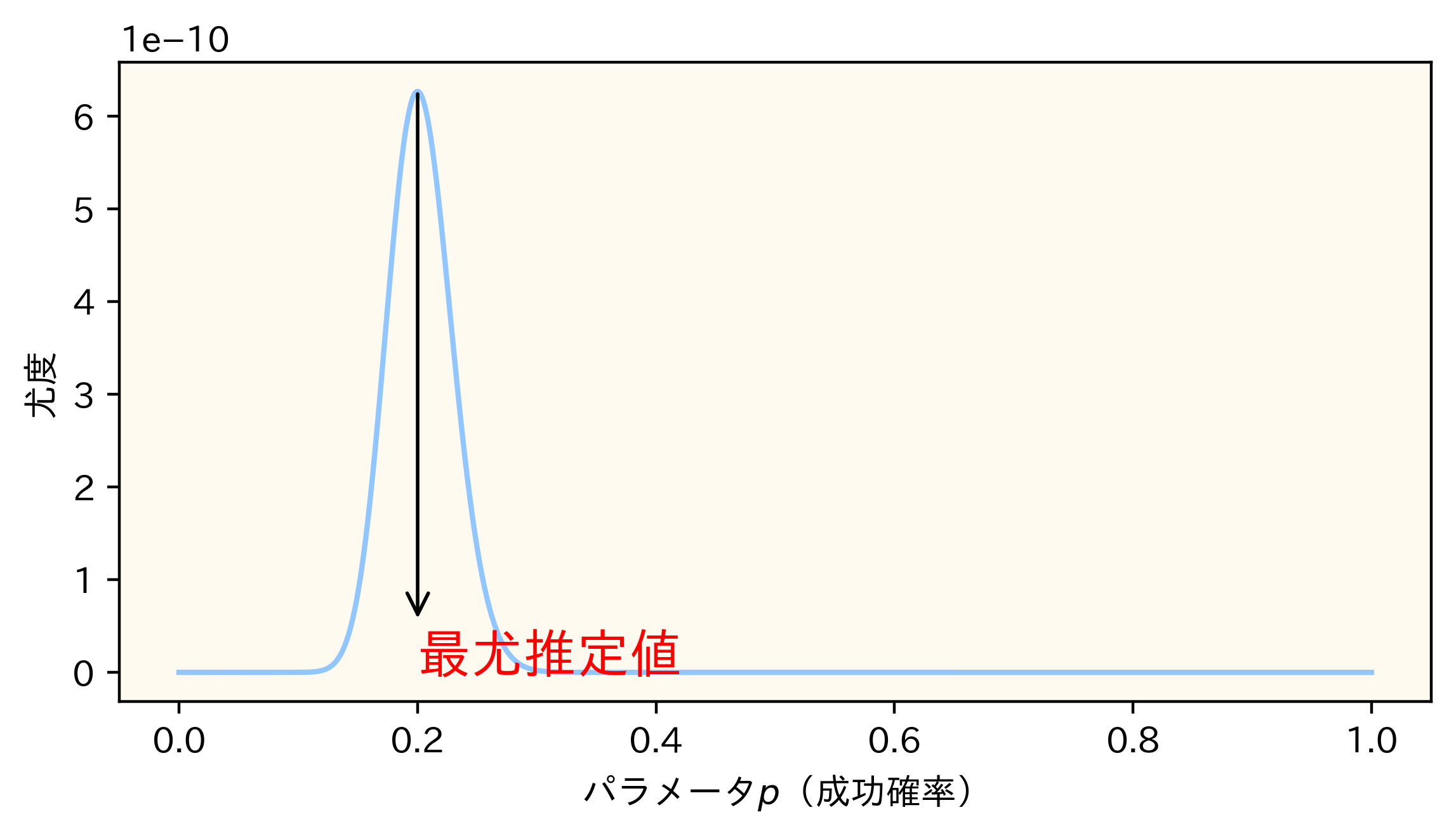
この尤度関数をもとにグラフを描画すると次のようになります。
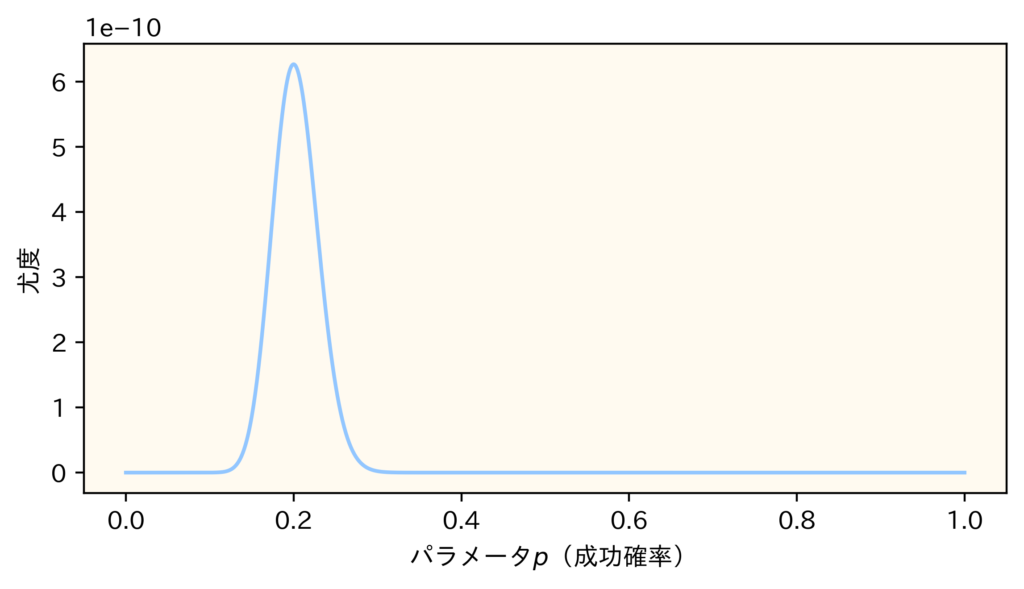
縦軸が尤度を表し、横軸がパラメータを表します。
グラフから読み取る最尤推定値
先ほどのグラフには山がありました。つまり、この山の頂点は尤度が最大となっているので、そのときパラメータ値が\(p\)の最尤推定値になります。今回の場合は\(p=0.2\)が最尤推定値ということです。
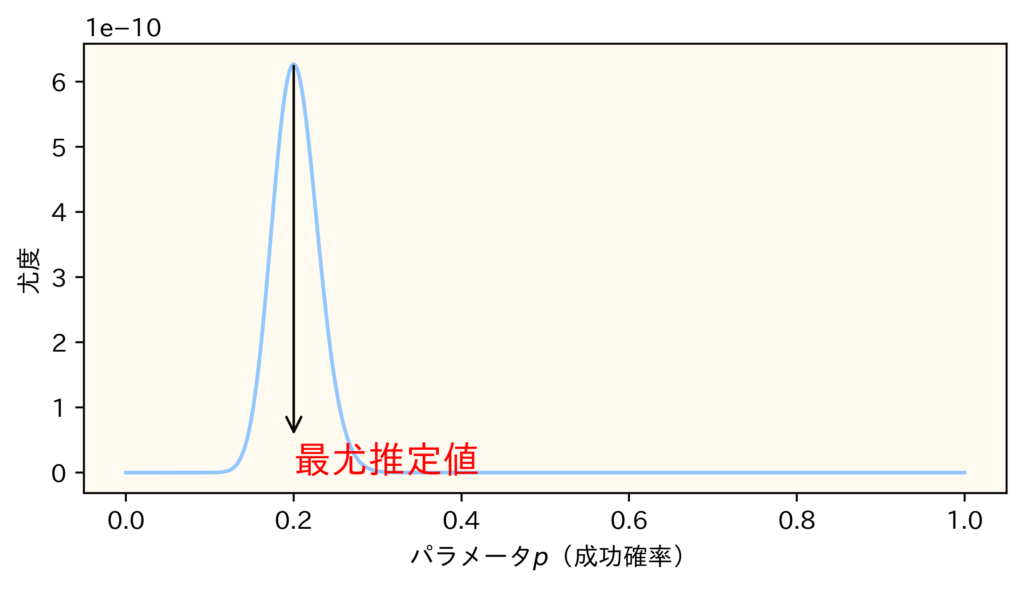
確認のために、最尤推定値を計算してみましょう。二項分布の成功確率\(p\)の最尤推定量は\(\frac{\bar{X}}{n}\)で与えられるので、今回の観測データ(11個)から推定される最尤推定値は
\begin{align}
\hat{p} &= \frac{\frac{\sum_{x}{x_i}}{11}}{20}\\
&= \frac{44/11}{20}\\
&= \frac{4}{20}\\
&= 0.2
\end{align}
$$
となります。グラフの山が頂点となるパラメータ値と最尤推定値が一致していることが確認できますね。二項分布の最尤推定量の証明が気になる方はこちらの記事を読んでみてください⇒「最尤法って何?」
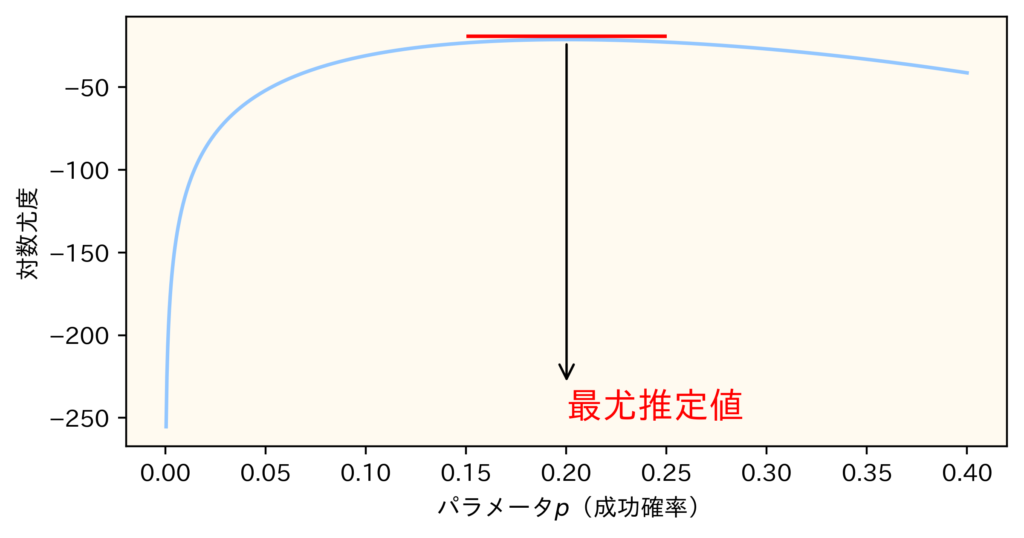
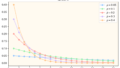
ちなみに対数尤度を可視化すると次のようになります。
今回は尤度関数を可視化することで尤度や最尤推定値といったものをグラフィカルに理解することができました。そのうち、尤度を用いた検定などについても投稿したいと思います。それでは今回は以上です。

コメント