幾何分布とは?
幾何分布(geometric distribution)は成功確率\(p\)のベルヌーイ試行を繰り返したとき、初めて成功するまでの回数が従う分布です。成功したときの試行を回数に含める場合と含めない場合がありますが、今回は成功したときの試行を回数に含める場合の幾何分布をメインで述べていきます。
幾何分布の定義
成功確率が\(p\)であるベルヌーイ試行を繰り返したとき、初めて成功するまでの試行回数を\(X\)とすると確率変数\(X\)は
$$
P(X=k) = p(1-p)^{k-1}\quad k=1,2,3,\cdots
$$
P(X=k) = p(1-p)^{k-1}\quad k=1,2,3,\cdots
$$
という確率分布に従う。この確率分布を幾何分布という。
期待値と分散
確率関数がわかったので、期待値と分散を求めていきましょう。先に結論から提示すると次の通りです。成功確率\(p\)が\(1\)に近いいほど期待値は小さく、成功確率が小さくなると急激に大きくなります。そして、分散も成功確率\(p\)が\(1\)に近いほど小さく、成功確率が小さくなると急激に大きくなります。
期待値・分散
確率変数\(X\)が幾何分布に従うとき
$$
\begin{align}
E[X] &= \frac{1}{p}\\
V[X] &= \frac{1-p}{p^2}
\end{align}
$$
\begin{align}
E[X] &= \frac{1}{p}\\
V[X] &= \frac{1-p}{p^2}
\end{align}
$$
証明はここをクリック↓
$$
\begin{align}
E[X] &= \sum_{k=1}^{\infty}k\cdot p(1-p)^{k-1}\\
&= p\sum_{k=1}^{\infty}k\cdot (1-p)^{k-1}\\
&= -p\sum_{k=1}^{\infty}\frac{d}{dp}(1-p)^{k}\\
&= -p\frac{d}{dp}\sum_{k=1}^{\infty}(1-p)^{k}\\
&= -p\frac{d}{dp}\frac{1}{1-(1-p)}\\
&= -p\frac{d}{dp}\frac{1}{p}\\
&= -p\left(-\frac{1}{p^2}\right)\\
&= \frac{1}{p}
\end{align}
$$
\begin{align}
E[X] &= \sum_{k=1}^{\infty}k\cdot p(1-p)^{k-1}\\
&= p\sum_{k=1}^{\infty}k\cdot (1-p)^{k-1}\\
&= -p\sum_{k=1}^{\infty}\frac{d}{dp}(1-p)^{k}\\
&= -p\frac{d}{dp}\sum_{k=1}^{\infty}(1-p)^{k}\\
&= -p\frac{d}{dp}\frac{1}{1-(1-p)}\\
&= -p\frac{d}{dp}\frac{1}{p}\\
&= -p\left(-\frac{1}{p^2}\right)\\
&= \frac{1}{p}
\end{align}
$$
$$
\begin{align}
E[X^2] = &= \sum_{k=1}^{\infty}k^2\cdot p(1-p)^{k-1}\\
&= -p\sum_{k=1}^{\infty}k\frac{d}{dp}(1-p)^{k}\\
&= -p\sum_{k=1}^{\infty}\{(k+1)-1\}\frac{d}{dp}(1-p)^{k}\\
&= -p\sum_{k=1}^{\infty}(k+1)\frac{d}{dp}(1-p)^{k}
+p\sum_{k=1}^{\infty}\frac{d}{dp}(1-p)^{k}\\
&= -p\sum_{k=1}^{\infty}\frac{d^2}{dp^2}(1-p)^{k+1} – E[X]\\
&= p\frac{d^2}{dp^2}\sum_{k=1}^{\infty}(1-p)^{k+1} – \frac{1}{p}\\
&= p\frac{d^2}{dp^2}\left(\frac{1}{p}-1\right) – \frac{1}{p}\\
&= p\frac{d^2}{dp^2}\frac{1-p}{p} – \frac{1}{p}\\
&= p\frac{2p}{p^4} – \frac{1}{p}\\
&= \frac{2}{p^2} – \frac{1}{p}\\
\end{align}
$$
\begin{align}
E[X^2] = &= \sum_{k=1}^{\infty}k^2\cdot p(1-p)^{k-1}\\
&= -p\sum_{k=1}^{\infty}k\frac{d}{dp}(1-p)^{k}\\
&= -p\sum_{k=1}^{\infty}\{(k+1)-1\}\frac{d}{dp}(1-p)^{k}\\
&= -p\sum_{k=1}^{\infty}(k+1)\frac{d}{dp}(1-p)^{k}
+p\sum_{k=1}^{\infty}\frac{d}{dp}(1-p)^{k}\\
&= -p\sum_{k=1}^{\infty}\frac{d^2}{dp^2}(1-p)^{k+1} – E[X]\\
&= p\frac{d^2}{dp^2}\sum_{k=1}^{\infty}(1-p)^{k+1} – \frac{1}{p}\\
&= p\frac{d^2}{dp^2}\left(\frac{1}{p}-1\right) – \frac{1}{p}\\
&= p\frac{d^2}{dp^2}\frac{1-p}{p} – \frac{1}{p}\\
&= p\frac{2p}{p^4} – \frac{1}{p}\\
&= \frac{2}{p^2} – \frac{1}{p}\\
\end{align}
$$
$$
\begin{align}
V[X] &= E[X^2] – (E[X])^2\\
&= \frac{2}{p^2} – \frac{1}{p} – \frac{1}{p^2}\\
&= \frac{1}{p^2} – \frac{p}{p^2}\\
&= \frac{1-p}{p^2}
\end{align}
$$
\begin{align}
V[X] &= E[X^2] – (E[X])^2\\
&= \frac{2}{p^2} – \frac{1}{p} – \frac{1}{p^2}\\
&= \frac{1}{p^2} – \frac{p}{p^2}\\
&= \frac{1-p}{p^2}
\end{align}
$$
おまけ:成功した試行を回数に含まない場合の期待値と分散
成功した試行を含まない場合の期待値と分散
確率変数\(Y\)が成功した試行を含まない場合の幾何分布に従うとき
$$
\begin{align}
E[Y] &= \frac{1-p}{p}\\
V[Y] &= \frac{1-p}{p^2}
\end{align}
$$
\begin{align}
E[Y] &= \frac{1-p}{p}\\
V[Y] &= \frac{1-p}{p^2}
\end{align}
$$
証明はここをクリック↓
確率変数\(X\)を成功した試行を回数に含む場合の幾何分布に従うとします。
$$
\begin{align}
E[Y] &= E[X-1]\\
& = E[X] – 1\\
& = \frac{1}{p} – 1\\
& = \frac{1-p}{p}\\
V[Y] &= V[X-1]\\
& = V[X]\\
& = \frac{1-p}{p^2}
\end{align}
$$
\begin{align}
E[Y] &= E[X-1]\\
& = E[X] – 1\\
& = \frac{1}{p} – 1\\
& = \frac{1-p}{p}\\
V[Y] &= V[X-1]\\
& = V[X]\\
& = \frac{1-p}{p^2}
\end{align}
$$
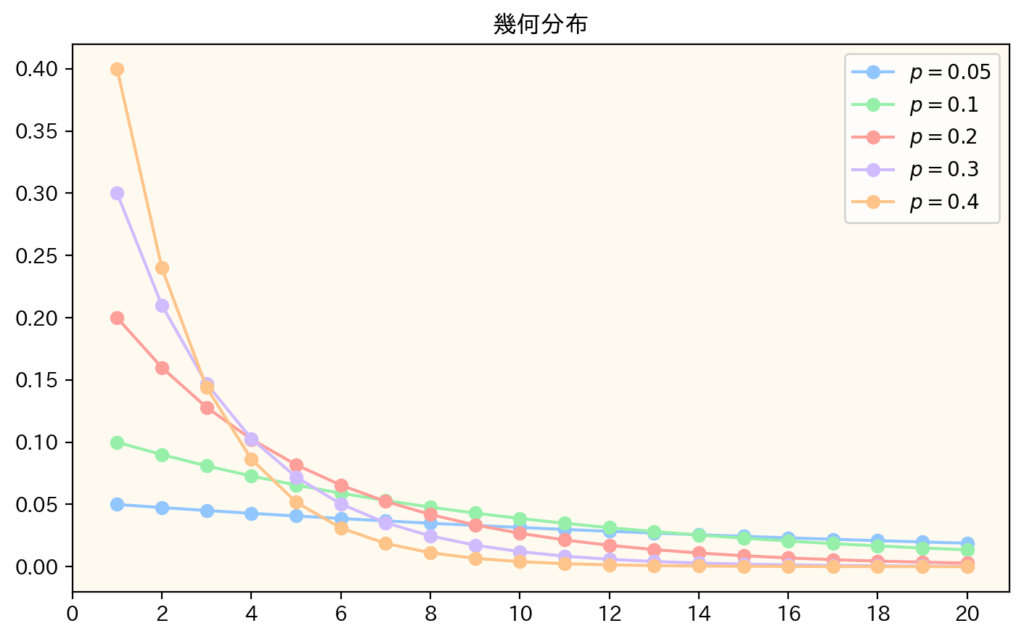
幾何分布のグラフ
これは成功確率\(p=0.05, 0.1, 0.2, 0.3, 0.4\)の幾何分布をそれぞれプロットしたグラフです。成功確率が高いものは早い段階で成功する確率が高く、成功するまでの試行回数が少し多くなると急激に確率が低くなります。逆に、成功確率が低いものは早い段階で成功する確率はあまり高くないですが、急激に確率が低下するような分布にではありません。とても当たり前なことですが、しっかりとグラフからも読み取れました。


コメント